Java-sorteringsalgoritm: Urvalssortering

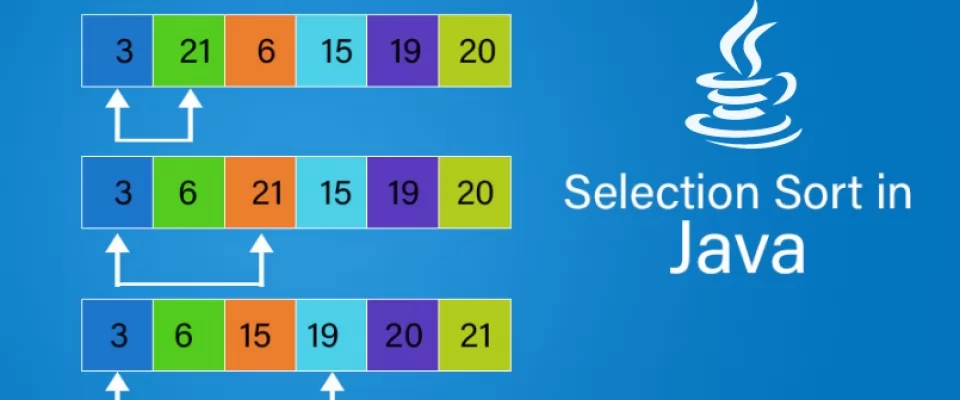
Idag ska vi analysera en sorteringsalgoritm som inte är särskilt effektiv men som ofta används inom olika områden. Vi pratar om Urval Sortera.

Låt oss ta en titt.

Intuition

Tanken bakom det är att dela upp arrayen för att sortera i två sub-arrayer: den första som innehåller den sorterade datan och upptar de första positionerna i arrayen medan den andra innehåller de data som måste sorteras och den upptar tendentiellt de slutliga positionerna av arrayen. I början är undersekvensen av sorterade element tom medan undersekvensen som representerar de osorterade elementen upptar hela arrayen.

Algoritmen väljer vid varje iteration minimum i osorterade sekvensen och placerar den i den sorterade undersekvensen. Proceduren fortsätter tills sekvensen av osorterade element inte är tom.

Låt oss titta på denna GIF:

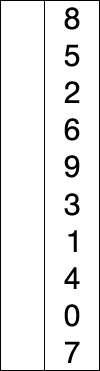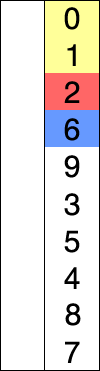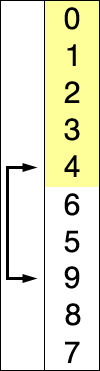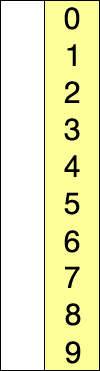
Flödesschema

Låt oss analysera algoritmens flödesschema, försiktigt givet av GeeksforGeeks.com.

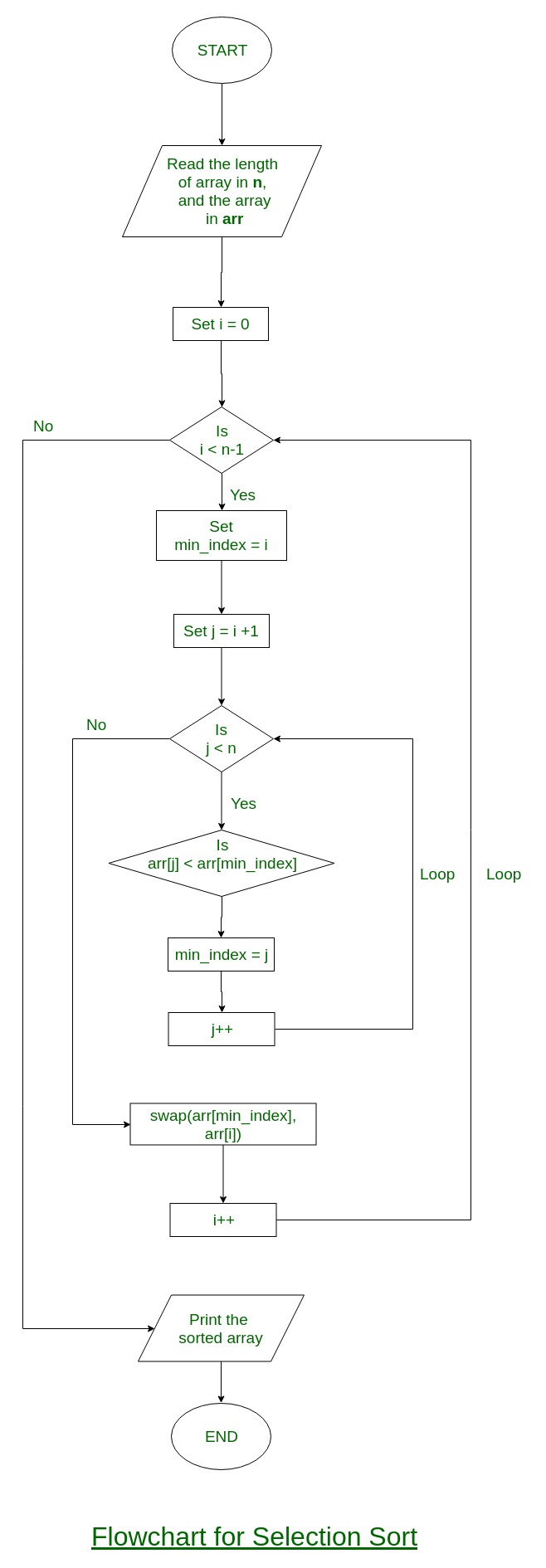
Det finns två grundläggande cykler som implementerar hela proceduren. Den första cykeln används för att hålla reda på i vilken position man ska infoga det minimum som vi har hittat medan den andra är van vid hitta minimum inom samlingen.

Genomförande

Låt oss ta en titt på implementeringen av algoritmen.

// Java-program för implementering av Selection Sort public class SelectionSort { public static void sort(int arr[]) { int n = arr.längd; for (int index = 0; index < n-1; index++) { // hitta minimielementet inom en osorterad array int min_idx = index; för (int j = index+1; j < n; j++) if (arr[j] < arr[min_idx]) min_idx = j; // byt minimum med // det aktuella elementet int temp = arr[min_idx]; arr[min_idx] = arr[index]; arr[index] = temp; } } public static void main(String args[]){ int arr[] = {64,25,12,22,11}; System.out.println("Osorterad array"); System.out.println(Arrays.toString(arr)); SelectionSort.sort(arr); System.out.println("Sorterad array"); System.out.println(Arrays.toString(arr)); } }

Låt oss förstå koden

Jag gjorde sorteringsmetoden statisk, som i de tidigare exemplen. Den första cykeln används för att hålla reda på den aktuella positionen för arrayen medan den innersta cykeln används för att söka efter minimum.

Sökandet efter minimum ska vara sekventiellt eftersom det inte finns några förutsättningar för att exempelvis kunna genomföra en dikotom sökning.

Nu ska vi analysera cyklerna som utgör algoritmen bättre

yttre cykel från 0 till arr.length-1: denna slinga håller reda på de effektiva iterationerna av proceduren, vilket också gör det möjligt att spåra positionen där det nya hittade minimumet kommer att placeras. Det “intressanta” är att det itererar till näst sista vektorns position. Motivationen är något trivial. När du når den sista positionen finns det inga fler element att byta den med, så det är värdelöst att göra en extra sväng. Det räcker med att stanna vid den näst sista positionen;
inre cykel: denna cykel används för att söka efter minimum i en del av arrayen, mer specifikt från index+1 till arr.length-1. Till skillnad från den externa slingan undersöker vi här även den sista positionen då den är en möjlig kandidat som ett minimum. Vi lagrar inte värdet av minimum utan snarare indexet som vi då behöver för utbytet.

I slutet finns utbytesförfarandet, som det är värt att lägga några ord på.

För en nybörjare kan variabeln med namnet temp verka onödig. Tvärtom är det oumbärligt, eftersom det tillåter oss att inte förlora värdet på en av de två variablerna efter den första tilldelningsoperationen. Faktum är att först sparar vi värdet på array [min_idx] i temp, sedan placerar vi den i array [min_idx] array [index [and finally in array [index] vi sätter temp. På detta sätt byts två variabler ut korrekt.

Rekursiv implementering

// Rekursivt Java-program för att sortera en array // med urval sortera public class RecursiveSelectionSort {// returnerar indexet för den minsta statiska int minIndex(int ​​a[], int index, int j) { if (index == j) return index; // hitta minimum bland de återstående elementen int k = minIndex(a, index + 1, j); // Returnera minimum av ström och återstående. återvända (a[index] < a[k])? index: k; } // rekursiv urvalssort. n är längden av a[] och index // är indexet för startelementet. public static void recurSelectionSort(int a[], int n, int index) { // Returnera när start och storlek är samma om (index == n) return; // anropar minimiindexfunktion för minimiindex int k = minIndex(a, index, n-1); // swap när index och index för minimum inte är samma om (k != index){ // swap int temp = a[k]; a[k] = a[index]; a[index] = temp; } // anropa metoden för urvalet rekursivt sortera recurSelectionSort(a, n, index + 1); } public static void main(String args[]) { int arr[] = {3, 1, 5, 2, 7, 0}; System.out.println("Osorterad array"); System.out.println(Arrays.toString(arr)); // anropa funktionen recurSelectionSort(arr, arr.length, 0); System.out.println("Sorterad array"); System.out.println(Arrays.toString(arr)); } }

Låt oss förstå koden

Denna algoritm är ganska väl lämpad för en rekursiv implementering. Låt oss analysera det bättre.

minIndex metod: den har som parametrar den vänstra och högra gränsen inom vilken det är nödvändigt att undersöka minimum. Basfallet är när slutet av de ej undersökta elementen har nåtts, så det returnerar det aktuella indexet. Den sista instruktionen används för att jämföra a[index] och a[k] och att returnera indexet för minimum mellan dem.
metoden recurSelectionSort: metoden har arrayen att sortera och två heltal som parametrar. De två siffrorna representerar längden på arrayen och positionen som vi undersöker. Proceduren är densamma för den iterativa versionen. Vi hittade minimum och vi byter ut det med den nuvarande positionen. Minimum hittas rekursivt som förklarats tidigare. Istället för en loop använder vi en rekursiv implementering för att kunna scrolla igenom arrayen. I själva verket, efter att ha gjort utbytet, kallas metoden rekursivt, men genom att öka index parameter, som representerar den aktuella positionen inom vilken miniminivån ska placeras.

Den huvudsakliga är densamma som den föregående, där vi skickar som parametrar arrayen att sortera, dess längd och 0 (startindex).

Komplexitet

Den interna cykeln är ett enkelt test för att jämföra det aktuella elementet med det minsta elementet som hittats hittills (plus koden för att öka indexet för det aktuella elementet och för att verifiera att det inte överskrider gränserna för arrayen). Elementens rörelse är utanför den interna cykeln: antalet utbyten är lika med (eftersom det sista elementet inte får bytas ut). Beräkningstiden bestäms av antalet jämförelser.

Sorteringen efter urval gör jämförelser och i värsta/bästa/genomsnittliga fall, utbyten.

Komplexiteten i en sådan algoritm är av

relaterade inlägg

Hur man använder endsWith-metoden i JavaScript

I den här korta handledningen ska vi se vad endsWith-metoden, introducerad i JavaScript ES6, är och hur den används med strängar i JavaScript. EndsWith-metoden är…

Återuppringningar i JavaScript

Callback-funktioner är samma gamla JavaScript-funktioner. De har ingen speciell syntax, eftersom de helt enkelt är funktioner som skickas som ett argument till en annan funktion. Funktionen som tar emot…

Hur man skapar PDF med JavaScript och jsPDF

Att skapa dynamiska PDF-filer direkt i webbläsaren är möjligt tack vare jsPDF JavaScript-biblioteket. I den sista delen av denna artikel har vi förberett en praktisk handledning där jag…

Alternativ för webbdesignverktyg med öppen källkod

Det finns många prototypverktyg, designverktyg för användargränssnitt eller vektorgrafikapplikationer. Men de flesta av dem är betalda eller stängda källor. Så här kommer jag att visa dig flera öppna…

Node.js och npm: introduktionshandledning

I den här handledningen kommer vi att se hur du installerar och använder både Node.js och npm-pakethanteraren. Dessutom kommer vi också att skapa en liten exempelapplikation. Om du…

Hur man ansluter till MySQL med Node.js

Låt oss se hur du kan ansluta till en MySQL-databas med Node.js, den populära JavaScript-runtime-miljön. Innan vi börjar är det viktigt att notera att du måste ha Node.js installerat…

JavaScript-programmeringsstilar: bästa praxis

När du programmerar med JavaScript finns det vissa konventioner som du bör tillämpa, speciellt när du arbetar i en teammiljö. Faktum är att det är vanligt att ha möten för att diskutera standarder…

Hemliga iPhone-koder för att låsa upp dolda funktioner

Vi älskar att våra enheter har dolda funktioner. Det är roligt att lära sig något nytt om tekniken vi använder varje dag, att upptäcka de där små funktionerna som inte annonseras av…

projekt